Optimization
An optimization problem is the problem of finding the best solution from all solutions. The theme of optimization shows up repeatedly in mathematics. What’s the shortest way to reach point X from point Z? What’s the fastest way to reach a given place from the current location?
1. Returning from a hike while on a camping trip, you see that your tent is on fire. Luckily you have a bucket in hand and you are near a river. What is the minimum total distance you will need to travel to get to the river and then to the tent?
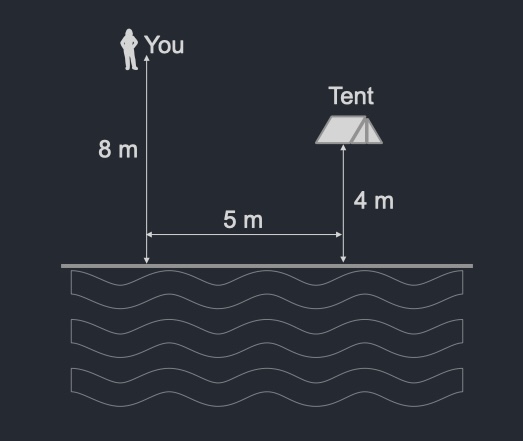
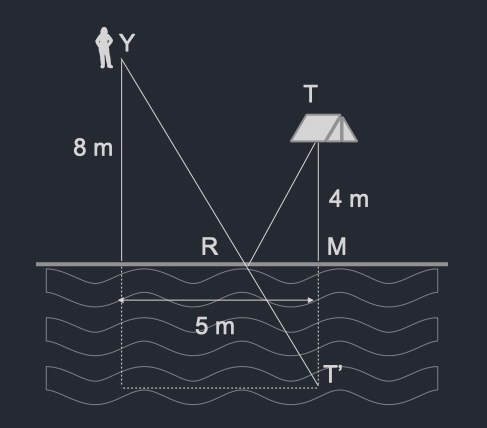
Let $Y$ denote your location and $T$ denote the tent's location. We need to choose a point $R$ in the river such that $YR+RT$ is minimized. Let $T'$ denote the image of $T$ about the river. Observe that $RT=RT'$ by Pythagoras' theorem. Therefore in order to minimize $YR+RT$, it suffices to minimize $YR+RT'$. The unique such $R$ is the point of intersection of $YT'$ and the river.
2. Two rectangles ABCD and DCEF of area 300 square cm each share one side (CD). What is the length of the side CD if the total length of all the 5 line segments (AB + BE + EF + FA + CD) is the smallest possible?
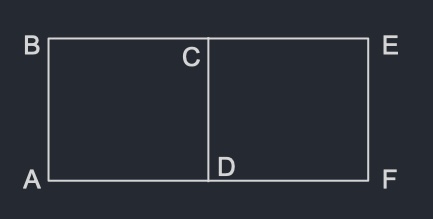
Let $a$ denote the length of AB (and CD and EF) and $b$ denote the length of AD (and BC). Since the two rectangles have equal area, it follows that the length of CE and DF is $b$. The objective is to find non-negative numbers $a$ and $b$ such that $3a+4b$ is minimized subject to the constraint that $a \times b=300$.
This problem is equivalent to the problem of finding $X$ (interepreted as $3a$) and $Y$ (interepreted as $4b$) such that $X+Y$ is minimized subject to the constraint that $X \times Y=3600$. For any two non-negative numbers $x$ and $y$, we can show that $x+y \geq 2 \sqrt{xy}$ with equality achieved if and only if $x=y$. Applying this result to our problem, we get $X=Y$. Since $X \times Y=3600$, it follows that $X=3a=60$ and so $a=20$.
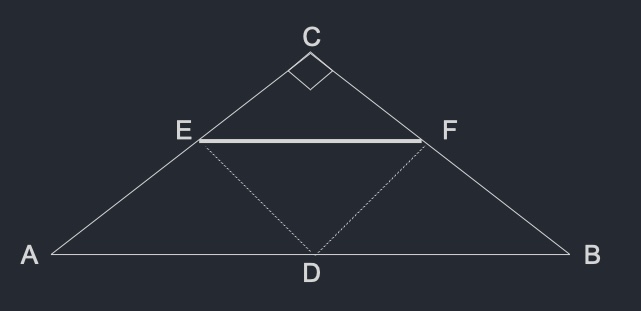
3. In the triangle ABC shown below, C is a right angle, D is any point on side AB. E and F are points on AC and BC respectively and are the foots of the perpendiculars from D to sides AC and BC. Where will you place D (on AB) to minimize EF? Justify your answer.

Observe that DECF is a rectangle and therefore its diagonals are equal. In order to choose D that minimizes EF, it is sufficient to choose D that minimizes CD. Therefore, D is the point on AB such that CD is perpendicular to it.
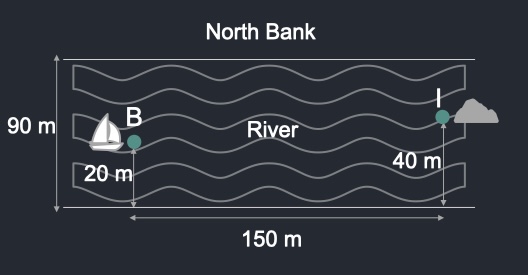
4. You are in a boat on a river at B with a passenger. You must first drop this passenger on the north bank and then pick up another passenger on the south bank and drop that passenger to an island I. You can drop the first passenger at any point N on the north bank, and you can ask the second passenger to wait at any point S on the south bank. What is the shortest total distance you will need to travel?
