Paradoxes
A paradox is a statement claiming something which goes against what is usually believed. Paradoxes may refer to one of the following.
- A logically correct argument leading to a statement claiming something which is contrary to one’s expectation. Eg: Monty Hall game (check out the session on probability for more details)
- A logically inconsistent result obtained even while properly applying accepted ways of reasoning. Eg: Russel’s paradox (check out the session on sets for more details)
- An argument establishing a false result due to a logically incorrect reasoning (fallacy). Eg: Zeno's paradoxes
Achilles and Tortoise Paradox
The great warrior Achilles and the tortoise decide to race to reach destination $D$. The total distance to travel is 3 metres. Achilles is known for his speed and therefore gives the tortoise a lead of 1 metre.
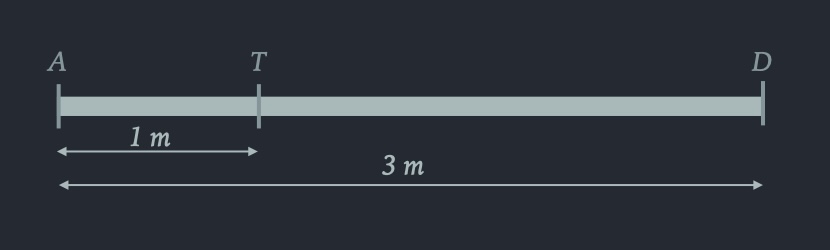
Reasoning 1:
- Distance (in metres) covered by tortoise after $t$ seconds = $1+t/2$
- Distance (in metres) covered by Achilles after $t$ seconds = $t$
- After 3 seconds, Achilles has covered 3 metres and tortoise has covered 2.5 metres.
- Therefore Achilles wins!
This reasoning seems plausible as Achilles is twice as fast as the tortoise and the initial head start is not enough for the tortoise to win. Let us infer a bit more about this race. Suppose Achilles overtakes the tortoise after $t$ seconds. Then $t=1+t/2$ and therefore $t=2$. That is, Achilles overtakes the tortoise after 2 seconds and the point of overtaking is 2 metres from the starting point A.
Reasoning 2:
- Achilles first has to reach tortoise’s starting point (Step 1) - in this time, the tortoise would have travelled a bit more
- Achilles now has to reach tortoise’s new position (Step 2) - in this time, the tortoise would have travelled a bit more
- ...
- For any positive integer $n$, after $n$ steps, Achilles is behind the tortoise
- Therefore, Achilles can never overtake the tortoise!
However, we all know that Achilles will win the race. Then where is the flaw in the reasoning? Let us analyze the steps in the argument carefully.
- At Step $0$, Achilles is at position $0$ (which is $0$ metres from starting point) and the tortoise is at position $1=2-1$ (which is $1$ metres from starting point).
- At Step $1$, Achilles's position is the position of the tortoise at Step $0$ (which is $1=2-1$) and the tortoise's position is $1.5 =2-1/2$.
- At Step $2$, Achilles's position is the position of the tortoise at Step $1$ (which is $1.5 =2-1/2$) and the tortoise's position is $1.75 =2-1/4$.
- ...
- At Step $k$, Achilles's position is the position of the tortoise at Step $k-1$ (which is $2-1/2^{k-1}$) and the tortoise's position is $2-1/2^k$. By taking limits, we can show that $\sum_{k=0}^{\infty} \frac{1}{2^k}=2$. It follows that this argument talks only about the first two seconds. And it wrongly concludes that Achilles can never overtake the tortoise while it should have only concluded that Achilles cannot overtake the tortoise in less than 2 seconds!
- https://plato.stanford.edu/
- https://en.wikipedia.org/wiki/Zeno's_paradoxes
Dichotomy Paradox
Before an object can travel a given distance, it must travel half the distance. In order to travel half the distance, it must travel 1/4 of the distance and so on. As this sequence goes on forever the distance cannot be traveled. What is the flaw in this reasoning?
The problem of the object reaching the destination can be viewed from a different perspective. If the object had reached the destination, then it would have had to travel the last 1/2 of the distance, and before that 1/4 of the distance, and before that 1/8 of the distance, and so on. Imagine winding time backwards and viewing the object getting ever-closer to the starting point. As an infinite number of steps cannot be completed, the object will never have moved from the starting point. Therefore any motion is impossible.
The resolution of the paradox awaited the proof (from calculus) that $\sum_{i=1}^{\infty}(1/2)^i=1$ and so the infinite number of *half-steps* needed to cover the distance (takes increasingly short amount of time) sums to a finite value leading to the conclusion that the total distance can be traversed.
Thomson's Lamp
Suppose we switch off a lamp. After 1 minute we switch it on. After $1/2$ a minute more we switch it off again, after a $1/4$ minute it is on, and so on. We know that summing each of these times gives rise to an infinite geometric series that converges to 2 minutes (by taking limits). When 2 minutes is up, is the lamp on or off?
It may seem absurd to claim that it is on since there is no previous time at which we turned the lamp on and left it on. Similarly, it cannot be off, since there is no previous time at which we turned the lamp off and left it off. However, it must be either on or off at the end of the two seconds. What is the problem with this reasoning?
Let us associate a number corresponding to the state of the lamp at any point in time: $0$ if it is off and $1$ if it is on. The initial state of the lamp is $0$ and call it the current state. Think of the act of turning the lamp on as adding 1 to the current state and the act of turning the lamp off as subtracting 1 from the current state. The act of switching the lamp on and off an infinite number of times is equivalent to the infinitely long sum $1-1+1-1+1-1+\ldots$.
Determining the answer regarding the state of the lamp after two seconds is equivalent to determining the value of this infinite sum. Using calculus, we can show that the value of this sum is undefined. Therefore, the lamp is neither on nor off at the end of two seconds.
Arrow Paradox
Consider an arrow in flight. For motion to occur, an object must change the position which it occupies. In any one (duration-less) instant of time, the arrow is neither moving to where it is, nor to where it is not. It cannot move to where it is not, because no time elapses for it to move there; it cannot move to where it is, because it is already there. In other words, at every instant of time there is no motion occurring. If everything is motionless at every instant and time is entirely composed of instants, then motion is impossible.
Resolving this paradox requires appeal to the theory of speed from calculus. This theory defines instantaneous motion, i.e., motion at an instant, without defining motion during an instant. This new treatment of motion says motion is being at different places at different times. The arrow gets from a point at time 1 to another point at time 2 simply in virtue of being at successive intermediate points at successive intermediate times. The arrow never changes its position during an instant but only over intervals composed of instants by occupying different positions at different times.