Basic Set Theory

Typically mathematical objects are often studied as collections. Examples: natural numbers, integers, real numbers, lines on a plane, triangles on a plane. Such collections are called sets. Intuitively, a set is a well-determined collection of distinct objects. The objects in a set are called elements or members of the set. The word well-determined in the definition refers to a specific property which makes it possible to identify whether a given object belongs to the set under consideration or not.

Membership

An object is a member of a set if it is one of the objects in the set. We use $\in$ to denote membership and $\notin$ to denote non-membership. For example, let $S$ be the set of all even integers from 1 to 10. Then 6 is an element of $S$ (denoted by $6 \in S$) but 5 is not (denoted by $5 \notin S$). The empty set is one that has no elements and it is denoted by $\emptyset$ or $\{\}$.

Notation

• A set may be specified by listing its elements enclosed by curly brackets separated by commas like $S=\{2,4,6,8,10\}$ and $Q=\{\{1\},1,2,3\}$.
• The ordering of the elements and the multiplicities of the elements in this notation are irrelevant.
• For sets with many elements, especially those following an implicit pattern, the list of members can be abbreviated using an ellipsis like $X=\{1,2,3,\ldots,10\}$ as long as the set under consideration is clear.
• Set-builder notation is a way of describing a set by stating the properties that its members must satisfy like $S=\{x \in \mathbb{N} : x \text{ is even}\}$ or $S=\{x \in \mathbb{N} : E(x)\}$ where $E(x)$ is the property that denotes $x$ is even.
• In the set-builder notation, the interpretation is that all values of $x$ for which the property holds (is true) belong to the set being defined and all values of $x$ for which the property does not hold (is false) do not belong to the set.

Operations on Sets

Following are the common operations on sets $X$ and $Y$.

1. Union $X \cup Y := \{z : z \in X \text{ or } z \in Y\}$.
2. Intersection $X \cap Y := \{z : z \in X \text{ and } z \in Y\}$.
3. Difference $X \setminus Y := \{z : z \in X \text{ and } z \notin Y\}$.
4. Symmetric difference $X \Delta Y := (X \setminus Y) \cup (Y \setminus X)$.
5. Given a set $U$ of all elements under consideration (called the universe), the complement of a set $X \subseteq U$ is $\overline{X}:=U \setminus X$.
6. Cartesian product $X \times Y := \{(x,y) : x \in X, y \in Y\}$ is the set of all ordered pairs $(x,y)$ where $x \in X$ and $y \in Y$.

Relationships between Sets

Consider two sets $X$ and $Y$. Following are the common relationships that can exists between $X$ and $Y$.

1. $X$ and $Y$ are said to be equal ($X=Y$) if they have same elements.
2. $X$ is a subset of $Y$ ($X \subseteq Y$) if each element of $X$ is an element of $Y$.
3. $X$ is a superset of $Y$ ($X \supseteq Y$) if each element of $Y$ is an element of $X$.
4. $X$ is a strict (or proper) subset of $Y$ ($X \subsetneq Y$) if $X \subseteq Y$ and $X \neq Y$.
5. $X$ is a strict (or proper) superset of $Y$ ($X \supsetneq Y$) if $X \supseteq Y$ and $X \neq Y$.
6. $X$ and $Y$ are said to be disjoint if $X \cap Y=\emptyset$ and overlapping otherwise.

The power set of a set $X$, denoted by $\mathcal{P}(X)$, is the set of all subsets of $X$. A partition of a set $X$ is a set of non-empty subsets of $X$ such that every element $x$ in $X$ is in exactly one of these subsets.

Venn Diagrams

Venn diagrams illustrate the relationship between two or more sets by using overlapping or non-overlapping circles (or ellipses) to represent sets.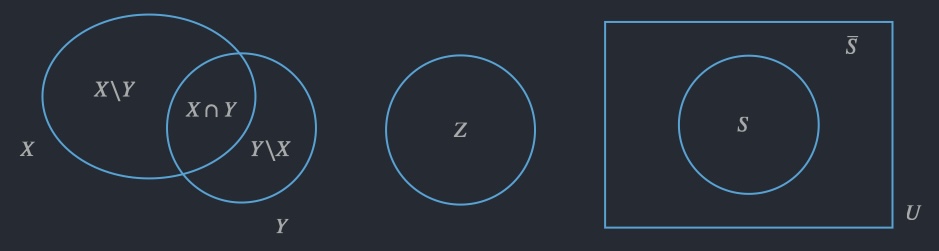

Russell's Paradox

While the intuitive definition of sets expresses our idea of sets, it has a problem. For any precisely-specified property, we may think that there is a set whose members are precisely those objects that satisfy the property. As examples, consider the set of all primes, the set of odd numbers, etc.

Call a set ordinary if it is not a member of itself. For example, the set of all points on a given line is not itself a point and so it is an ordinary set. Every set is either ordinary or not ordinary. All sets that we come across are ordinary and it is questionable whether there are any sets that are not ordinary. What about the collection of all sets? In any case, ordinary sets exists. Let $\mathcal{O}$ be the collection of all ordinary sets. Is $\mathcal{O}$ ordinary or not? If $\mathcal{O}$ is ordinary then $\mathcal{O}$ contains $\mathcal{O}$ (since $\mathcal{O}$ is the set of all ordinary sets) leading to the conclusion that $\mathcal{O}$ is not ordinary. On the other hand, if $\mathcal{O}$ is not ordinary then $\mathcal{O}$ contains $\mathcal{O}$ (by the definition of ordinary sets) leading to the conclusion that $\mathcal{O}$ is ordinary.

Therefore, if $\mathcal{O}$ is ordinary then $\mathcal{O}$ is not ordinary which in turn implies that $\mathcal{O}$ is ordinary and so on. This logically inconsistent result obtained even while properly applying accepted ways of reasoning is called as Russell's paradox. This leads us to conclude that $\mathcal{O}$ cannot exist. This paradox implies that the definition of set is unsatisfactory and we need to be precise while defining any mathematical primitive.

Mathematicians came up with a statement of the conditions under which sets are formed to avoid paradoxes like Russell's paradox. These conditions are called Zermelo-Fraenkel condtions with axiom of choice (ZFC conditions). We will not mention these conditions here but state the following properties of these conditions.

• Do not allow a set corresponding to every property.
• Do not allow a set to contain itself.
• Do not allow a set containing all sets.

Now we are ready to state the definition of a set. A set is a well-determined collection of distinct objects that satisfies the ZFC conditions.